[packetwars 2019] Writeup 'Fun with Finite Fields'

Heidelberg, Germany, after a lovely day in march at the TROOPERS Conference 2019 I find myself in a traditional german restaurant. It’s cold, it’s loud, the food is 6/10, I’m sober and me and Parzel are waiting for Packetwars to start.

Nice! A crypto challenge! “Fun with Finite Fields” is the name.

The only prior information about the challenge is the name: “Fun with Finite Fields” - OK probably Elliptic Curve cryptography… I’m scared - I only know one (textbook) attack on EC signatures. That’s all I need, as I will find out.

How the challenge works:

We find the lonely challenge server waiting for my TCP connection. I get this prompt after connecting with netcat:

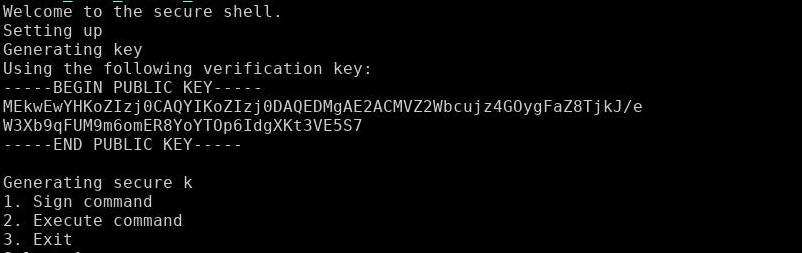
Note the display of the public key - we will need that for later.

‘Generating secure k’ - What a surprise, this is probably the textbook example I was thinking about. How the attack works will unfold shortly, but let’s look first what the server has to offer.

Two commands of interest:

• Sign command: Enter a command and retrieve it’s EC crypto signature.
• Execute command:  Enter a command and it’s signature and retrieve it’s output.

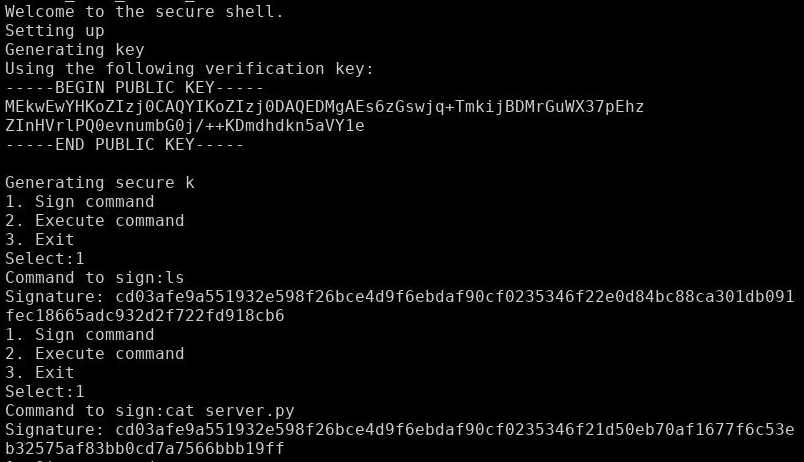
Alright, let’s execute ‘ls’:

Pretty straight forward: The challenge clearly wants us to forge a signature for a ‘cat flag.txt’ command.

Let’s see what server.py looks like (execute ‘cat server.py’):

import ecdsa
import os
import sys
import secrets

print("Welcome to the secure shell.")
print("Setting up")
print("Generating key")

sk = ecdsa.SigningKey.generate() # uses NIST192p
vk = sk.get_verifying_key()

print("Using the following verification key:")
print(vk.to_pem().decode('utf-8'))


"""https://en.wikipedia.org/wiki/Elliptic_Curve_Digital_Signature_Algorithm#Security says it is important to have a secure random k
so make sure we generate it properly"""
print("Generating secure k")
k = secrets.randbelow(sk.curve.order)

def sign():
    allowed_cmds = ['ls', 'pwd', 'cat server.py']
    cmd = input("Command to sign:")
    if cmd not in allowed_cmds:
        print("Illegal command, only allowed commands are %s" % allowed_cmds)
    else:
        sig = sk.sign(cmd.encode("utf-8"), k=k)
        print("Signature: %s" % sig.hex())

def execute():
    cmd = input("Command to execute: ")
    signature = input("Signature: ")
    signature = bytes.fromhex(signature)
    try:
        vk.verify(signature, cmd.encode('utf-8'))
        print("Correct signature, executing command")
        os.system(cmd)
    except ecdsa.BadSignatureError:
        print("Invalid signature")
    return

menu = {
    '1': sign,
    '2': execute,
    '3': sys.exit
}
while True:
    print("1. Sign command")
    print("2. Execute command")
    print("3. Exit")
    cmd = input("Select:")
    try:
        menu[cmd]()
    except KeyError:
        print("Invalid selection")

The textbook vulnerability is right there: k is not generated randomly for each signature but only once and reused for different signatures!

BTW: Nice hint in the code:
https://en.wikipedia.org/wiki/Elliptic_Curve_Digital_Signature_Algorithm
It states there:
As the standard notes, it is not only required for k to be secret, but it is also crucial to select different k for different signatures, otherwise the equation in step 6 can be solved for the private key.

La solución:

All we need to do is follow the instructions on Wikipedia:

Let’s resolve the symbols here:

• n : group order (all operations are mod n)
• k : cryptographically secure random integer from [1,n-1]
• z : SHA1(message) mod n, where message will be signed (SHA1 is default)
• (r, s) : the signature of message (yes the signature is a tuple)

How the attack works:

Using the public key from the greeting message, we can infer n, the group order.
We just need to parse the public key, which is best done within python-ecdsa.

We also need to parse the 2 signatures we obtained from the ‘ls’ and ‘cat server.py’ commands.
Additionally we compute z and z’ by hashing ‘ls’ and ‘cat server.py’ with SHA1.

We can then compute k and finally the private key.
Using the private key, we finally can forge signatures to commands of our choice.

Attack and results:

Let’s feed the public key and the 2 signatures into our python script:

import ecdsa
import gmpy

pub_key_string = "MEkwEwYHKoZIzj0CAQYIKoZIzj0DAQEDMgAEs6zGswjq+TmkijBDMrGuWX37pEhzZInHVrlPQ0evnumbG0j/++KDmdhdkn5aVY1e"

m1 = "ls"
sig1 = "cd03afe9a551932e598f26bce4d9f6ebdaf90cf0235346f22e0d84bc88ca301db091fec18665adc932d2f722fd918cb6"

m2 = "cat server.py"
sig2 = "cd03afe9a551932e598f26bce4d9f6ebdaf90cf0235346f21d50eb70af1677f6c53eb32575af83bb0cd7a7566bbb19ff"

# Generate own key-pair to access utility functions
sk = ecdsa.SigningKey.generate() # uses NIST192p
vk = sk.get_verifying_key()

# Parse public key from the server and obtain n
veri_key = vk.from_pem(pub_key_string)
n = veri_key.pubkey.order

# Parse the 2 signatures
r1, s1 = ecdsa.util.sigdecode_string(bytes.fromhex(sig1), order=n)
r2, s2 = ecdsa.util.sigdecode_string(bytes.fromhex(sig2), order=n)

# Hash the commands (ls, cat server.py) and transform them into numbers
h1 = ecdsa.keys.sha1(m1.encode("utf-8"))
z1 = ecdsa.util.string_to_number(h1.digest())
h2 = ecdsa.keys.sha1(m2.encode("utf-8"))
z2 = ecdsa.util.string_to_number(h2.digest())

# Perform math according to wikipedia
k=((z1 - z2) * gmpy.invert(s1 - s2, n)) % n
print("k: ", k)
r_inv = gmpy.invert(r1,n)
d_a = ((s1*k - z1) * r_inv) % n

# Sign own command (cat flag.txt) using the obtained secret exponent
COMMAND = "cat flag.txt"
sk_new = sk.from_secret_exponent(d_a)
print("Command: ", COMMAND)
sig = sk_new.sign(COMMAND.encode("utf-8"), k=k)
print("Signature: ", sig.hex())

The forged signature to our own command (‘cat flag.txt’) is presented to the server:

That’s it: The flag is right there!

All in all I must say, the only big challenge was to fiddle with python-ecdsa to parse the public key and signatures.
It’s nice to work with python-ecdsa and get familiar with the library since I have not worked much with Elliptic Curve cryptography.
I definitely learned alot about the framework and how use it.
I hope someone will find help in the textbook implementation of this attack.

Cheers

Niknax